
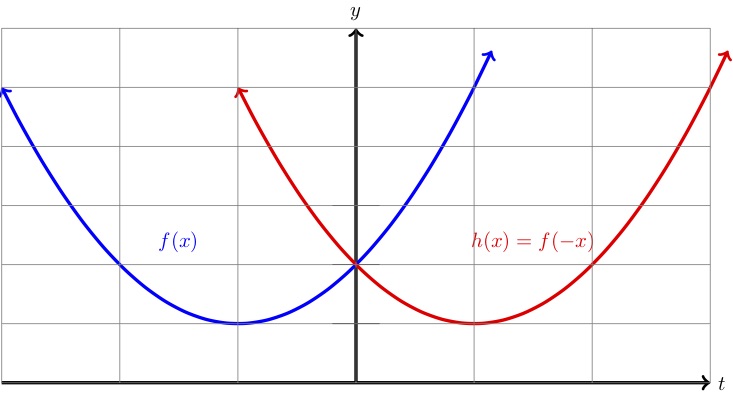
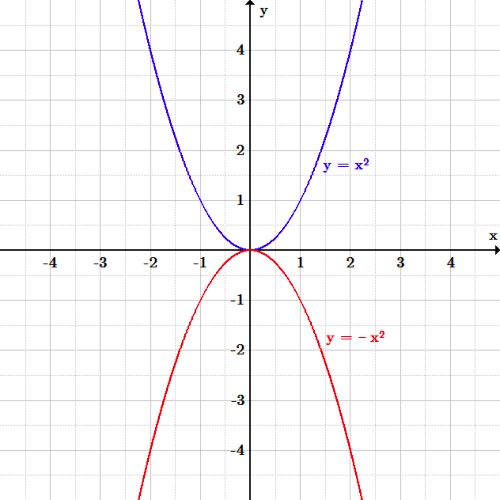
What would happen if you change the signs of the ordered pair?Īfter the 10 minutes of partner work time, students complete the final check for understanding independently.What does it mean to reflect a point over an axis?.How did you know that was the correct name of the coordinate pair?.How did you know to draw the coordinate pair in that particular place?.Are scholars correctly describing the similarities and differences between two points that are reflections of one-another?.Are scholars accurately describing what happens when you switch the sign of the values in a coordinate pair?.Are scholars correctly identifying the coordinate pair’s reflection with and without a grid?.
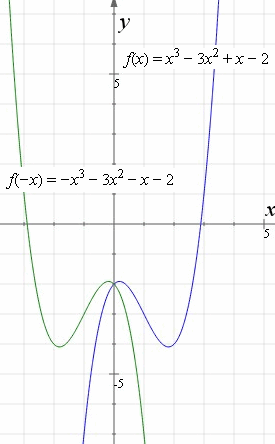
Are scholars correctly plotting the coordinate pair on the grid?.Are scholars correctly labeling all of the necessary components of the coordinate graph?.As they are working, I circulate around the room. Students work on the Partner Practice problem set for 10 minutes. Students share out, and then I ask for the group to make a conjecture about the relationship of the coordinates when we reflect over the x-axis. When we reflect a point over the y-axis, what do you notice about the relationship between the x- and y-values of the coordinates of each point? Once, we've gone through the same process for the other two ordered pairs in this section, I have students turn and talk with their partner about a generalization we can make about reflections. Then we are going to count that same number of units going away from the y-axis and plot and label my point with the coordinate pair (-4, 5). We know that the y-axis represents 0, so therefore both points have the same absolute value, or distance from 0. The following graphs are symmetric about (a) re ection across the x-axis (b) re ection across the y-axis (c) re ection about the origin. Once students name that the point is 4 units away from the axis, I tell them that the reflection is going to be the same distance from the y axis but in the opposite direction. Testing for symmetry for graphs of equations A graph is called Symmetric with respect to a re ection if that re ection does not change the graph. I want to spend time on the conceptual idea of reflecting a point, so we don't jump right into simply using the opposite value for the x-coordinate. Students annotate the problem by boxing the words 'y-axis.' My expectation is that they always box the axis over which we're rotating, as a small way to help them not reflect over the incorrect axis.įor this first point, (4, 5), I ask students to count how many units it takes to get from the y-axis to the point. Together, we plot the first point, (4, 5) and label it as Point A. We label the origin, the x- and y-axis, and all four quadrants. I have a copy of the INM materials on the document camera, and I ask for students to give me the names of the important pieces. To begin this section of the lesson, I have students help me label the parts of the graph.


 0 kommentar(er)
0 kommentar(er)
